Current Electricity Ques 114
- The actual value of resistance $R$, shown in the figure is $30$ $ \Omega$. This is measured in an experiment as shown using the standard formula $R=\frac{V}{I}$, where $V$ and $I$ are the readings of the voltmeter and ammeter, respectively. If the measured value of $R$ is $5 \%$ less, then the internal resistance of the voltmeter is
(2019 Main, 10 Jan II))

(a) $600 $ $\Omega$
(b) $570 $ $\Omega$
(c) $350 $ $\Omega$
(d) $35 $ $\Omega$
Show Answer
Answer:
Correct Answer: 114.(b)
Solution:
Formula:
- Measured value of $R=5 \%$ less than actual value of $R$.
Actual values of $R=30$ $ \Omega$
So, measured value of $R$ is
$R^{\prime} =30-(5 \% \text { of } 30)=30-\frac{5}{100} \times 30 $
$\Rightarrow \quad R^{\prime} =28.5$ $ \Omega $
Now, let us assume that internal resistance of voltmeter $R _V$. Replacing voltmeter with its internal resistance, we get following circuit.
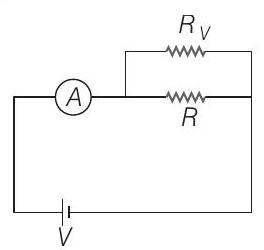
It is clear that the measured value, $R^{\prime}$ should be equal to parallel combination of $R$ and $R _V$. Mathematically,
$R^{\prime} =\frac{R R _V}{R+R _V}=28.5 \Omega $
$\text { Given, } \quad R =30 \Omega \Rightarrow \frac{30 R _V}{30+R _V}=28.5 $
$\Rightarrow \quad 30 R _V =(28.5 \times 30)+28.5 R _V $
$\Rightarrow \quad 1.5 R _V =28.5 \times 30 $
$\Rightarrow \quad R _V =\frac{28.5 \times 30}{1.5}=19 \times 30 \text { or } R _V=570 $ $\Omega$





