Current Electricity Ques 21
- In an experiment, the resistance of a material is plotted as a function of temperature (in some range). As shown in the figure, it is a straight line.
(2019 Main, 10 April I)
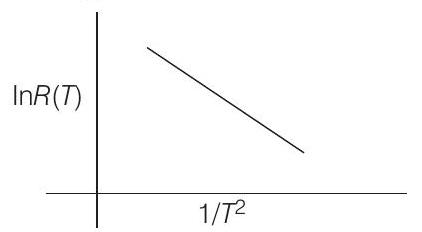
One may conclude that
(a) $R(T)=R _0 e^{-T^{2} / T _0^{2}}$
(b) $R(T)=R _0 e^{T^{2} / T _0^{2}}$
(c) $R(T)=R _0 e^{-T _0^{2} / T^{2}}$
(d) $R(T)=\frac{R _0}{T^{2}}$
Show Answer
Answer:
Correct Answer: 21.(c)
Solution:
Formula:
- From the given graph,
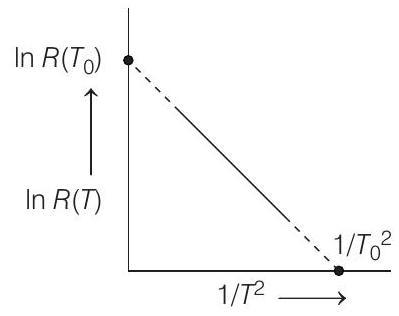
We can say that, $\ln R(T) \propto-\frac{1}{T^{2}}$
Negative sign implies that the slope of the graph is negative.
$ \begin{array}{ll} \text { or } & \ln R(T)=\text { constant }(-\frac{1}{T^{2}}) \\ \Rightarrow & \ln R(T)=\frac{\exp (\text { const. })}{\exp (\frac{1}{T^{2}})} \\ \Rightarrow & \ln R(T)=R _0 \exp (-\frac{T _0^{2}}{T^{2}}) \end{array} $
Alternate Solution
From graph,
$ \frac{\frac{1}{T^{2}}}{\frac{1}{T _0^{2}}}+\frac{\ln R(T)}{\ln R\left(T _0\right)}=1 $
$\Rightarrow \quad \ln R(T)=\left[\ln R\left(T _0\right)\right] \cdot [1-\frac{T _0{ }^{2}}{T^{2}}]$
or
$ R(T)=R _0 \exp (\frac{-T _0^{2}}{T^{2}}) $





