Current Electricity Ques 40
- In the circuit shown below, the key is pressed at time $t=0$. Which of the following statement(s) is (are) true?
(2016 Adv.)
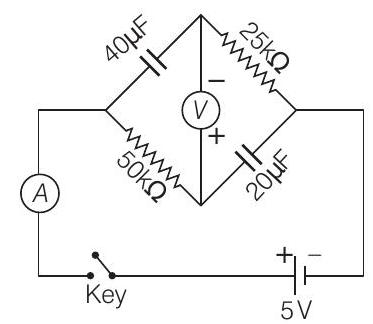
(a) The voltmeter display $-5$ $ V$ as soon as the key is pressed and displays $+5$ $ V$ after a long time
(b) The voltmeter will display $0$ $ V$ at time $t=\ln 2$ seconds
(c) The current in the ammeter becomes $1/e$ of the initial value after $1$ second
(d) The current in the ammeter becomes zero after a long time
Show Answer
Answer:
Correct Answer: 40.(a,b,c,d)
Solution:
Formula:
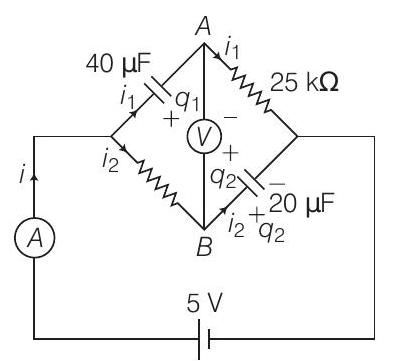
Just after pressing key,
$ \begin{aligned} & 5-25000 i _1=0 \\ & 5-50000 i _2=0 \end{aligned} $
(As charge in both capacitors)
$ \begin{aligned} & \Rightarrow \quad i _1=0.2 mA \Rightarrow i _2-0.1 mA \\ & \text { And } \quad V _B+25000 i _1=V _A \\ & \Rightarrow \quad V _B-V _A=-5 V \end{aligned} $
After a long time, $i _1$ and $i _2=0$ (steady state)
$\Rightarrow \quad 5-\frac{q _1}{40} =0 $
$\Rightarrow \quad q _1 =200 \mu C $
$5-\frac{q _2}{20} =0 \Rightarrow q _2=100 \mu C $
$V _B-\frac{q _2}{20} =V _A $
$\Rightarrow \quad V _B-V _A =+5 V$
$\Rightarrow$ Option (a) is correct.
For capacitor 1, $q _1=200\left[1-e^{-t / 1}\right] \mu C$
$ i _1=\frac{1}{5} e^{-t / 1} mA $
For capacitor $2, q _2=100\left[1-e^{-t / 1}\right] \mu C$
$ i _2=\frac{1}{10} e^{-t / 1} mA $
$\Rightarrow \quad V _B-\frac{q _2}{20}+i _1 \times 25=V _A $
$\Rightarrow \quad V _B-V _A=5\left[1-e^{-t}\right]-5 e^{-t}=-5\left[1-2 e^{-t}\right] $
$\text { At } \quad t=\ln 2, V _B-V _A=5[1-1]=0$
$\Rightarrow$ Option (b) is correct.
At $t=1, i=i _1+i _2=\frac{1}{5} e^{-1}+\frac{1}{10} e^{-1}=\frac{3}{10} \cdot \frac{1}{e}$
At $t=0, \quad i=i _1+i _2=\frac{1}{5}+\frac{1}{10}=\frac{3}{10}$
$\Rightarrow \quad $ (c) is correct.
After a long time, $i _1=i _2=0$
$\Rightarrow \quad$ Option (d) is correct.





