Current Electricity Ques 47
- An infinite ladder network of resistances is constructed with $1 $ $\Omega$ and $2 $ $\Omega$ resistances, as shown in figure.
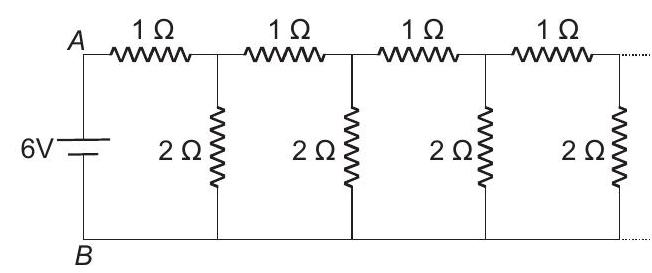
The $6$ $ V$ battery between $A$ and $B$ has negligible internal resistance.
(1987, 7M)
(a) Show that the effective resistance between $A$ and $B$ is $2 $ $\Omega$.
(b) What is the current that passes through the $2 $ $\Omega$ resistance nearest to the battery?
Show Answer
Answer:
Correct Answer: 47.(b) $ 1.5 $ $A$
Solution:
Formula:
- (a) Let $R _{A B}=x$. Then, we can break one chain and connect a resistance of magnitude $x$ in place of it.
Thus, the circuit remains as shown in figure.
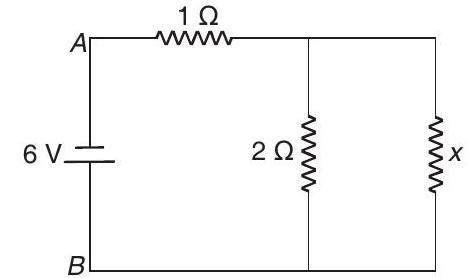
Now, $2 x$ and $x$ are in parallel. So, their combined resistance is $\frac{2 x}{2+x}$
$ \text { or } \quad R _{A B}=1+\frac{2 x}{2+x} $
But $R _{A B}$ is assumed as $x$. Therefore,
$ x=1+\frac{2 x}{2+x} $
Solving this equation, we get
$ x=2 \Omega $
Hence proved.
(b) Net resistance of circuit $R=1+\frac{2 \times 2}{2+2}=2 $ $\Omega$
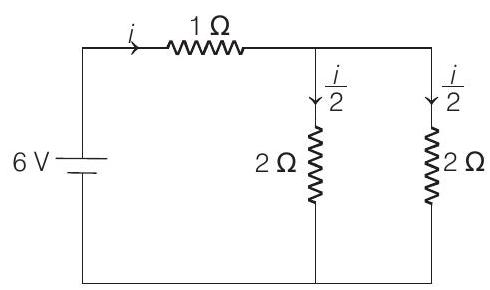
$\therefore$ Current through battery $i=\frac{6}{2}=3 A$
This current is equally distributed in $2 $ $\Omega$ and $2 $ $\Omega$ resistances. Therefore, the desired current is $\frac{i}{2}$ or $1.5$ $ A$.





