Current Electricity Ques 49
- In the circuit shown in figure $E _1=3 $ $V, E _2=2 $ $V$, $E _3=1 $ $V$ and $R=r _1=r _2=r _3=1 $ $ \Omega$.
$(1981,6 M)$
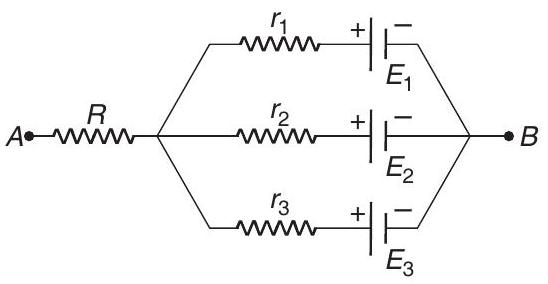
(a) Find the potential difference between the points $A$ and $B$ and the currents through each branch.
(b) If $r _2$ is short-circuited and the point $A$ is connected to point $B$, find the currents through $E _1, E _2, E _3$ and the resistor $R$.
Show Answer
Answer:
Correct Answer: 49.$ (a) 2 V ,1 A , 0,-1A \quad (b) 1A, 2A,-1A,2A$
Solution:
Formula:
- (a) Equivalent emf of three batteries is calculated based on their configuration (series or parallel)
$ E _{eq}=\frac{\sum(E / r)}{\Sigma(1 / r)}=\frac{(3 / 1+2 / 1+1 / 1)}{(1 / 1+1 / 1+1 / 1)}=3 $ $V $
Further $r_1, r_2$ and $r_3$ each are of $1$ $ \Omega$. Therefore, internal resistance of the equivalent battery will be $\frac{1}{3}$ $ \Omega$ as all three are in parallel.
The equivalent circuit is therefore shown in the given figure.
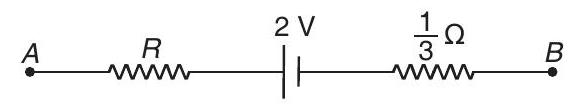
Since, no current is drawn from the battery.
$ \begin{alignedat} & \qquad V _{A B}=2 V(\text { From } V=E - i r) \\ & \text { Further, } V _{A B}+V _A-V _B=E _1-i _1 r _1 \\ & \therefore \quad i _1=\frac{V _B-V _A+E _1}{r _1}=\frac{-2+3}{1}=1 A \\ & \text { Similarly, } i _2=\frac{V _B-V _A+E _2}{r _2}=\frac{-2+2}{1}=0 \\ & \text { and } \quad i _3=\frac{V _B-V _A+E _3}{r _3}=\frac{-2+1}{1}=-1 A \end{aligned} $
(b) $r_2$ is short circuited means resistance of this branch becomes zero. Making a closed circuit with a battery and resistance $R$. Applying Kirchhoff’s voltage law in three loops so formed.
$49-i _1-\left(i _1+i _2+i _3\right)=0 \quad …….(i) $
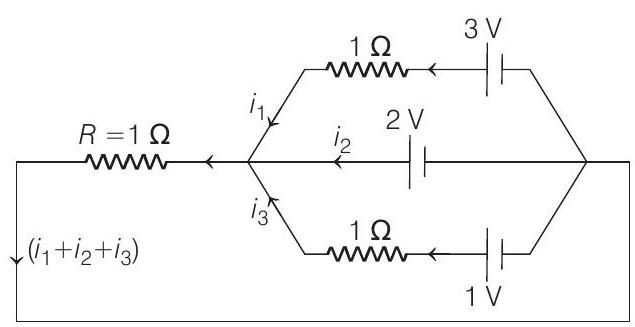
$ \begin{aligned}49-\left(i_1+i_2+i_3\right) & =0 \quad …….(ii)\49-i_3-\left(i_1+i_2+i_3\right) & =0 \quad …….(iii) \end{aligned} $
From Eq. (ii) $\quad i _1+i _2+i _3=2$ $ A$
$\therefore \quad$ Substituting in Eq. (i), we get, $i_1=1$ $A$
Substituting in Eq. (iii) we get, $i _3=-1$ $ A$
$ \therefore \quad i _2=2 $ $A $





