Current Electricity Ques 53
- In a Wheatstone bridge (see figure), resistances $P$ and $Q$ are approximately equal. When $R=400$ $ \Omega$, the bridge is balanced. On interchanging $P$ and $Q$, the value of $R$ for balance is $405$ $ \Omega$. The value of $X$ is close to
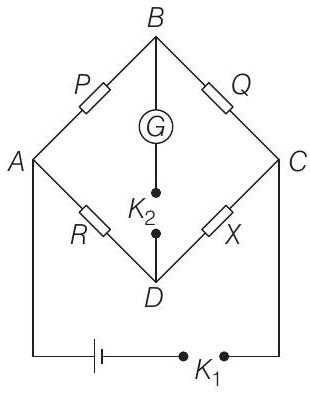
(2019 Main, 11 Jan I)
(a) $404.5 $ $\Omega$
(b) $401.5 $ $\Omega$
(c) $402.5 $ $\Omega$
(d) $403.5 $ $\Omega$
Show Answer
Answer:
Correct Answer: 53.(c)
Solution:
Formula:
- For a balanced Wheatstone bridge,
$ \frac{P}{R}=\frac{Q}{X} $
In first case when $R=400 $ $\Omega$, the balancing equation will be
$ \begin{aligned} \frac{P}{R} & =\frac{Q}{X} \Rightarrow \frac{P}{400 \Omega}=\frac{Q}{X} \\ \Rightarrow \quad P & =\frac{400 \times Q}{X} \quad …….(i) \end{aligned} $
In second case, $P$ and $Q$ are interchanged and $R=405 \Omega$
$ \begin{aligned} & \therefore \quad \frac{Q}{R}=\frac{P}{X} \\ & \Rightarrow \quad \frac{Q}{405}=\frac{P}{X} \quad …….(ii) \end{aligned} $
Substituting the value of $P$ from Eq. (i) in Eq. (ii), we get
$ \frac{Q}{405}=\frac{Q \times 400}{X^{2}} $
$ \begin{array}{ll} \Rightarrow & X^{2}=400 \times 405 \\ \Rightarrow & X=\sqrt{400 \times 405}=402.5 \end{array} $
The value of $X$ is close to $402.5 $ $\Omega$.





