Current Electricity Ques 56
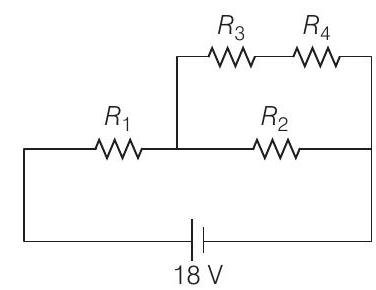
- In the given circuit, the internal resistance of the $18 V$ cell is negligible. If $R _1=400$ $ \Omega, R _3=100$ $ \Omega$ and $R _4=500$ $ \Omega$ and the reading of an ideal voltmeter across $R _4$ is $5$ $ V$, then the value of $R _2$ will be
(2019 Main, 9 Jan II)
(a) $550 $ $\Omega$
(b) $230 $ $\Omega$
(c) $300 $ $\Omega$
(d) $450 $ $\Omega$
Show Answer
Answer:
Correct Answer: 56.(c)
Solution:
Formula:
- According to question, the voltage across $R _4$ is 5 volt, then the current across it
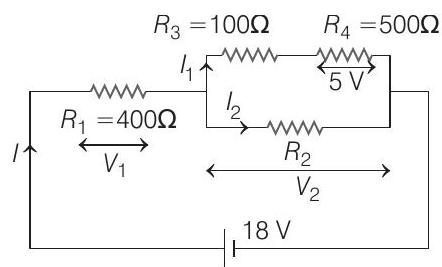
According to Ohm’s law,
$\Rightarrow \quad V=I R \quad \Rightarrow \quad 5=I _1 \times R _4 $
$\Rightarrow \quad 5=I _1 \times 500 $
$I _1=\frac{5}{500}=\frac{1}{100} A$
The potential difference across series combination of $R _3$ and $R _4$
$\Rightarrow \quad V _2=\left(R _3+R _4\right) I=600 \times \frac{1}{100}=6$ Volt
So, potential difference (across $R _1$ )
$ V _1=18-6=12 V $
Current through $R _1$ is,
$ I=\frac{V _1}{R _1}=\frac{12}{400}=\frac{3}{100} A $
So current through $R _2$ is,
$ I _2=I-I _1=\frac{3}{100}-\frac{1}{100} A=\frac{2}{100} A $
Now, from $V=I R$, we have,
$ R _2=\frac{V _2}{I _2}=\frac{6}{(2 / 100)}=300$ $ \Omega $





