Current Electricity Ques 58
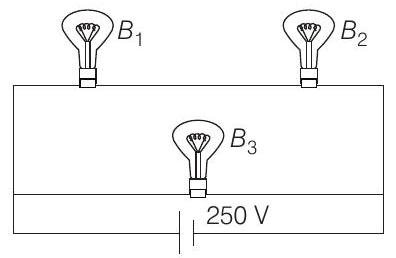
- A $100$ $ W$ bulb $B _1$, and two $60 $ $W$ bulbs $B _2$ and $B _3$, are connected to a $250 $ $V$ source, as shown in the figure. Now $W _1, W _2$ and $W _3$ are the output powers of the bulbs $B _1, B _2$ and $B _3$ respectively. Then,
(2002, 2M)
(a) $W_1 > W_2 = W_3$
(b) $W _1>W _2>W _3$
(c) $W _1<W _2=W _3$
(d) $W _1<W _2<W _3$
Show Answer
Answer:
Correct Answer: 58.(d)
Solution:
Formula:
- $\quad P=\frac{V^{2}}{R}$ so, $R=\frac{V^{2}}{P}$
$ \therefore \quad R _1=\frac{V^{2}}{100} \quad \text { and } \quad R _2=R _3=\frac{V^{2}}{60} $
$ \text { Now, } \quad W _1=\frac{(250)^{2}}{\left(R _1+R _2\right)^{2}} \cdot R _1 $
$ \begin{gathered} W _2=\frac{(250)^{2}}{\left(R _1+R _2\right)} \cdot R _2 \quad \text { and } \quad W _3=\frac{(250)^{2}}{R _3} \\ W _1: W _2: W _3=15: 25: 64 \text { or } W _1<W _2<W _3 \end{gathered} $





