Current Electricity Ques 62
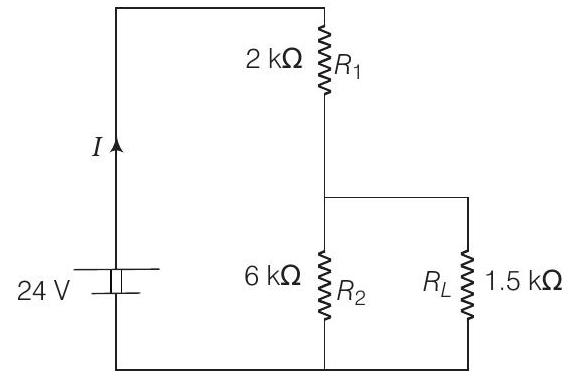
- For the circuit shown in the figure
(2009)
Show Answer
Answer:
Correct Answer: 62.(a,d)
Solution:
- $R _{\text {total }}=2+\frac{6 \times 1.5}{6+1.5}=3.2 $ $k \Omega$
(a) $I=\frac{24 V}{3.2 k \Omega}=7.5 mA=I _{R _1}$
$I _{R _2}=(\frac{R _L}{R _L+R _2} )I$
$I=\frac{1.5}{7.5} \times 7.5=1.5 $ $ mA$
$ I _{R _L}=6$ $ mA $
(b) $V _{R _L}=\left(I _{R _L}\right)\left(R _L\right)=9$ $ V$
(c) $\frac{P _{R _1}}{P _{R _2}}=\frac{\left(I _{R _1}^{2}\right) R _1}{\left(I _{R _2}^{2}\right) R _2}=\frac{(7.5)^{2}(2)}{(1.5)^{2}(6)}=\frac{25}{3}$
(d) When $R _1$ and $R _2$ are inter changed, then
$ \frac{R _2 R _L}{R _2+R _L}=\frac{2 \times 1.5}{3.5}=\frac{6}{7} k \Omega $
Now potential difference across $R _L$ will be
$ V _L=24 [\frac{6 / 7}{6+6 / 7}]=3$ $ V $
Earlier it was $9$ $ V$
Since, $\quad P=\frac{V^{2}}{R} \quad$ or $\quad P \propto V^{2}$
In new situation potential difference has been decreased three times. Therefore, power dissipated will decrease by a factor of $9$.





