Current Electricity Ques 64
- A cell of internal resistance $r$ drives current through an external resistance $R$. The power delivered by the cell to the external resistance will be maximum when
(8 April 2019, II)
(a) $R=2 $ $r$
(b) $R=$ $r$
(c) $R=0.001 $ $r$
(d) $R=1000 $ $r$
Show Answer
Answer:
Correct Answer: 64.(b)
Solution:
Formula:
- Given circuit is shown in the figure below
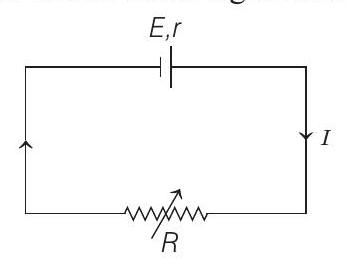
Net current, $\quad I=\frac{E}{R+r}$
Power across $R$ is given as
$ P=I^{2} R=(\frac{E}{R+r})^{2} \cdot R \quad \text { [using Eq. (i ) }] $
For the maximum power,
$ \frac{d P}{d R}=0 $
$\Rightarrow \quad \frac{d P}{d R}=\frac{d}{d R} \left((\frac{E}{R+r})^2 \cdot R\right) $
$=\quad E^{2} \frac{d}{d R} \left(\frac{R}{(R+r)^{2}} \right) $
$=\quad E^{2} \left[\frac{(R+r)^{2} \times 1-2 R \times(R+r)}{(R+r)^{4}}\right]=0 $
$\Rightarrow \quad(R+r)^{2}=2 R(R+r) \text { or } R+r=2 R \Rightarrow r=R$
$\therefore$ The power delivered by the cell to the external resistance is maximum when $R=r$.
Alternate Solution
From maximum power theorem, power dissipated will be maximum when internal resistance of source will be equals to external load resistance, i.e.
$r=R$.





