Current Electricity Ques 71
- In a meter bridge experiment, the circuit diagram and the corresponding observation table are shown in figure
(2019 Main, 10 April I)
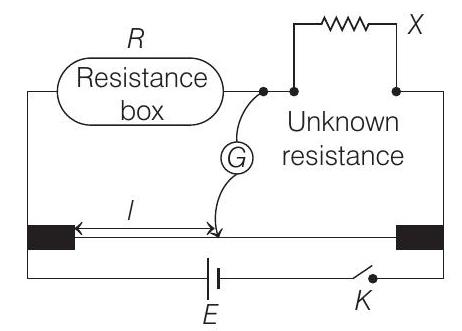
| S. No. | $R(\Omega)$ | $l(cm)$ |
|---|---|---|
| 1. | 1000 | 60 |
| 2. | 100 | 13 |
| 3. | 10 | 1.5 |
| 4. | 1 | 1.0 |
Which of the readings is inconsistent?
(a) $3$
(b) $2$
(c) $1$
(d) $4$
(a) the current $I$ through the battery is $7.5$ $ mA$
(b) the potential difference across $R _L$ is $18$ $ V$
(c) ratio of powers dissipated in $R _1$ and $R _2$ is $ 3$
(d) if $R _1$ and $R _2$ are interchanged, magnitude of the power dissipated in $R _L$ will decrease by a factor of $ 9$
Show Answer
Answer:
Correct Answer: 71.(d)
Solution:
Formula:
- Unknown resistance ’ $X$ ’ in meter bridge experiment is given by
$ X=(\frac{100-l}{l}) R $
Case (1) When $R=1000 \Omega$ and $l=60$ $ cm$, then
$ X=\frac{(100-60)}{60} \times 1000=\frac{40 \times 1000}{60} $
$ \Rightarrow \quad X=\frac{2000}{3} \Omega \approx 667 \Omega $
Case (2) When $R=100 \Omega$ and $l=13$ $ cm$, then
$ \begin{aligned} \quad \quad \quad X=(\frac{100-13}{13}) \times 100 \\ =\frac{100 \times 87}{13}=\frac{8700}{13} \Omega \approx 669 \Omega \end{aligned} $
Case (3) When $R=10 \Omega$ and $l=1.5$ $ cm$, then
$ \begin{aligned} X & =(\frac{100-1.5}{1.5}) \times 10 \\ & =\frac{98.5}{1.5} \times 10=\frac{9850}{15} \Omega \approx 656 \Omega \end{aligned} $
Case (4) When $R=1 \Omega$ and $l=1.0$ $ cm$, then
$ \begin{aligned} & X=(\frac{100-1}{1}) \times 1 \\ \therefore \quad & X =99 \Omega \end{aligned} $
Thus, from the above cases, it can be concluded that, value calculated in case (4) is inconsistent.





