Current Electricity Ques 72
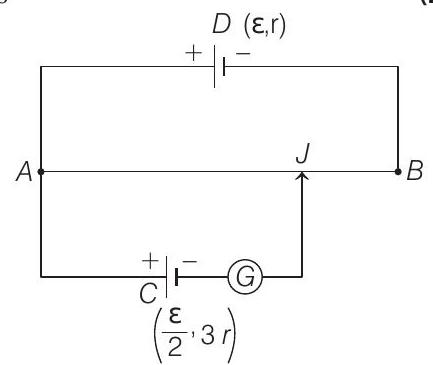
- A potentiometer wire $A B$ having length $L$ and resistance $12$ $ r$ is joined to a cell $D$ of EMF $\varepsilon$ and internal resistance $r$. A cell $C$ having emf $\frac{\varepsilon}{2}$ and internal resistance $3$ $ r$ is connected. The length $A J$ at which the galvanometer as shown in figure shows no deflection is
(2019 Main, 10 Jan I)
(a) $\frac{5}{12} $ $L$
(b) $\frac{11}{12} $ $L$
(c) $\frac{13}{24} $ $L$
(d) $\frac{11}{24} $ $L$
Show Answer
Answer:
Correct Answer: 72.(c)
Solution:
Formula:
- Given, length of potentiometer wire $(A B)=L$
Resistance of potentiometer wire $(A B)=12 $ $r$
EMF of cell $D$ of potentiometer $=\varepsilon$
Internal resistance of cell ’ $D$ ’ $=r$
EMF of cell ’ $C$ ’ $=\frac{\varepsilon}{2}$
Internal resistance of cell ’ $C$ ’ $=3 r$
Current in potentiometer wire
$ \begin{aligned} i & =\frac{\text { EMF of cell of potentiometer }}{\text { Total resistance of potentiometer circuit }} \\ \Rightarrow i & =\frac{\varepsilon}{r+12 r}=\frac{\varepsilon}{13 r} \end{aligned} $
Potential drop across the balance length $A J$ of potentiometer wire is
$ \begin{aligned} \Rightarrow \quad V _{A J} & =i \times R _{A J} \\ V _{A J} & =i \quad \begin{aligned} \text { (Resistance per unit length of } \\ \text { potentiometer wire } \times \text { length } A J) \end{aligned} \\ \Rightarrow \quad V _{A J} & =i (\frac{12 r}{L} \times x) \end{aligned} $
where, $x$ =balance length $A J$.
As null point occurs at $J$ so potential drop across balance length $A J=$ EMF of the cell ’ $C$ ‘.
$\Rightarrow V _{A J} =\frac{\varepsilon}{2} $
$\Rightarrow (i \frac{12 r}{L} \times x) =\frac{\varepsilon}{2}$
$\Rightarrow \frac{\varepsilon}{13 r} \times \frac{12 r}{L} \times x =\frac{\varepsilon}{2} $
$\Rightarrow x =\frac{13}{24} $ $L$





