Current Electricity Ques 93
- A galvanometer whose resistance is $50$ $ \Omega$, has $25$ divisions in it. When a current of $4 \times 10^{-4} A$ passes through it, its needle (pointer) deflects by one division. To use this galvanometer as a voltmeter of range $2.5 $ $V$, it should be connected to a resistance of
(Main 2019, 12 Jan II)
(a) $250$ $ \Omega$
(b) $6200$ $ \Omega$
(c) $200$ $ \Omega$
(d) $6250$ $ \Omega$
Show Answer
Answer:
Correct Answer: 93.(c)
Solution:
Formula:
- Current for deflection of pointer by
1 division $=4 \times 10^{-4} A$
So, current for full-scale deflection $=I _g$ $=$ Number of divisions $\times$ Current for 1 division
$\Rightarrow \quad I _g=25 \times 4 \times 10^{-4}=1 \times 10^{-2} A$
Now, let a resistance of $R$ is put in series with galvanometer to make it a voltmeter of range $2.5 V$.
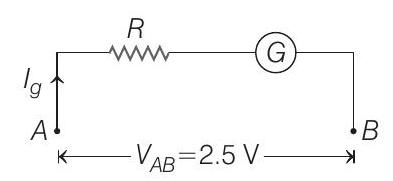
Then,
$ \begin{aligned} I _g(R+G) & =V _{A B} \\ 1 \times 10^{-2}(R+50) & =2.5 \end{aligned} $
$\left[\because\right.$ Given, $\left.G=50 \Omega, V _{A B}=2.5 V\right]$
$\therefore \quad R=250-50=200$ $ \Omega$





