Current Electricity Ques 99
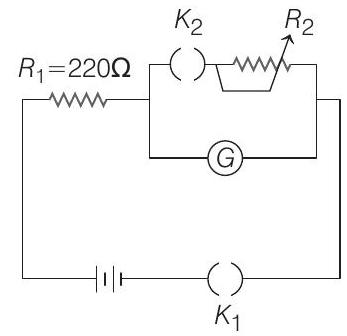
- The galvanometer deflection, when key $K _1$ is closed but $K _2$ is open equals $\theta _0$ (see figure). On closing $K _2$ also and adjusting $R _2$ to $5 $ $\Omega$, the deflection in galvanometer becomes $\frac{\theta _0}{5}$. The resistance of the galvanometer is given by (neglect the internal resistance of battery) :
(Main 2019, 12 Jan I)
(a) $22 $ $\Omega$
(b) $5 $ $\Omega$
(c) $25 $ $\Omega$
(d) $12 $ $\Omega$
Show Answer
Answer:
Correct Answer: 99.(a)
Solution:
Formula:
- For a galvanometer, $i _g \propto \theta$ or $i _g=C \theta$
where, $I _g=$ current through coil of galvanometer,
$\theta$ = angle of deflection of coil
and $C$ is the constant of proportionality.
Now, $K _1$ is closed and $K _2$ is opened, circuit resistance is
$ R _{eq}=R _1+R _g $
where, $R _g=$ galvanometer resistance.
Hence, galvanometer current is
i.e.,
$ i _g=\frac{V}{R _1+R _g} $
where, $V=$ supply voltage.
As deflection is given $\theta _0$, we have
$ i _g=\frac{V}{R _1+R _g}=C \theta _0 \quad …….(i) $
When both keys $K _1$ and $K _2$ are closed, circuit resistance.
$ R _{eq}=R _1+(\frac{R _2 \times R _g}{R _2+R _g}) $
Current through galvanometer will be
$ \begin{aligned} i _{g _2} & =\frac{V}{R _1+\frac{R _2 R _g}{R _2+R _g}} \times \frac{R _2}{\left(R _2+R _g\right)} \\ & =\frac{V R _2}{R _1 R _2+R _1 R _g+R _2 R _g}=C \cdot \frac{\theta _0}{5} \quad …….(ii) \end{aligned} $
Now, dividing Eq. (i) by Eq. (ii), we get
$ \frac{R _1 R _2+R _1 R _g+R _2 R _g}{R _2\left(R _1+R _g\right)}=5 $
Substituting $R _1=220 $ $\Omega$ and $R _2=5 $ $\Omega$,
we get
$\frac{1100+220 R _g+5 R _g}{5\left(220+R _g\right)} =5 $
$1100+225 R _g =5500+25 R _g $
$\Rightarrow \quad 200 R _g =4400$
$\Rightarrow \quad R _g=\frac{4400}{200}=22 \Omega $
$\therefore \quad R _g=22 $ $\Omega$





