knowledge-route Maths10 Ch6
title: “Lata knowledge-route-Class10-Math1-2 Merged.Pdf(1)” type: “reveal” weight: 1
TRIGONOMETRY
TRIGONOMETRY
11.1 TRIGONOMETRY :
Trigonometry means, the science which deals with the measurement of triangles.
11.1 (a) Trigonometric Ratios :
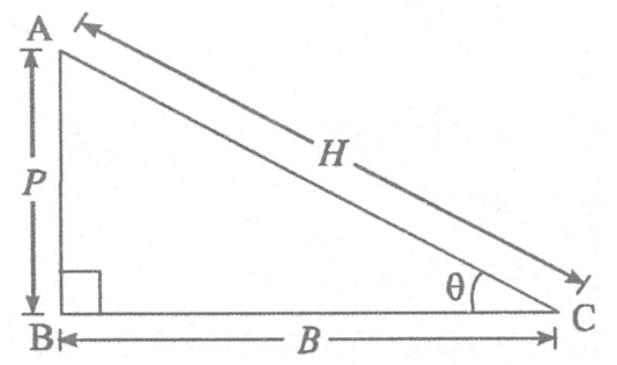
A right angled triangle is shown in Figure. $\angle B$ Is of $90^{\circ}$ Side opposite to $\angle B$ be called hypotenuse. There are two other angles i.e. $\angle A$ and $\angle C$. It we consider $\angle C$ as $\theta$, then opposite side to this angle is called perpendicular and side adjacent to $\theta$ is called base.
TRIGONOMETRY
(i) Six Trigonometry Ratio are :
$ \begin{matrix} \sin \theta=\frac{\text { Perpenicular }}{\text { Hypotenuse }}=\frac{P}{H}=\frac{A B}{A C} & cosec \theta=\frac{\text { Hypoteuse }}{\text { Perpendicular }}=\frac{H}{P}=\frac{A C}{A B} \\ \cos \theta=\frac{\text { Base }}{\text { Hypotenuse }}=\frac{B}{H}=\frac{B C}{A C} & \sec \theta=\frac{\text { Hypotenuse }}{\text { Base }}=\frac{H}{B}=\frac{A C}{B C} \\ \tan \theta=\frac{\text { Perpendicular }}{\text { Base }}=\frac{P}{B}=\frac{A B}{B C} & \cot \theta=\frac{\text { Base }}{\text { Parpendicular }}=\frac{B}{P}=\frac{B C}{A B} \end{matrix} $
TRIGONOMETRY
(ii) Interrelationship is Basic Trigonometric Ratio :
$ \begin{matrix} \tan \theta=\frac{1}{\cot \theta} \Rightarrow & \cot \theta=\frac{1}{\tan \theta} \\ \cos \theta=\frac{1}{\sec \theta} \Rightarrow & \sec \theta=\frac{1}{\cos \theta} \\ \sin \theta=\frac{1}{cosec \theta} \Rightarrow & cosec \theta=\frac{1}{\sin \theta} \end{matrix} $
We also observe that
$\tan \theta=\frac{\sin \theta}{\cos \theta} \Rightarrow \cot \theta=\frac{\cos \theta}{\sin \theta}$
TRIGONOMETRY
11.1 (b) Trigonometric Table :
| $\theta \to$ | $\mathbf{0}$ | $30^{0}$ | $45^{0}$ | $60^{0}$ | $90^{0}$ |
|---|---|---|---|---|---|
| Sin | $\mathbf{0}$ | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ | $\mathbf{1}$ |
| Cos | $\mathbf{1}$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ | $\mathbf{0}$ |
| Tan | $\mathbf{0}$ | $\frac{1}{\sqrt{3}}$ | $\mathbf{1}$ | $\sqrt{3}$ | Not defined |
| Cot | Not defined |
$\sqrt{3}$ | $\mathbf{1}$ | $\frac{1}{\sqrt{3}}$ | $\mathbf{0}$ |
| Sec | $\mathbf{1}$ | $\frac{2}{\sqrt{3}}$ | $\sqrt{2}$ | $\mathbf{2}$ | Not defined |
| Cosec | Not defined |
$\mathbf{2}$ | $\sqrt{2}$ | $\frac{2}{\sqrt{3}}$ | $\mathbf{1}$ |
$$$$
TRIGONOMETRY
11.1 (c) Trigonometric Identities :
(i) $ \sin ^{2} \theta+\cos ^{2} \theta=1$
(A) $\sin ^{2} \theta=1-\cos ^{2} \theta$
(B) $\cos ^{2} \theta=1-\sin 2 \theta$
(ii) $1+\tan ^{2} \theta=\sec ^{2} \theta$
(A) $\sec ^{2} \theta-1=\tan ^{2} \theta$
(B) $\sec ^{2} \theta-\tan ^{2} \theta=1$
(C) $\tan ^{2} \theta-\sec ^{2} \theta=-1$
(iii) $1+\cot ^{2} \theta=cosec^{2} \theta$
(A) $cosec^{2} \theta-1=\cot ^{2} \theta$
(B) $ cosec^{2} \theta-\cot ^{2} \theta=1$
(C) $\cot ^{2} \theta-cosec^{2} \theta=-1$
TRIGONOMETRY
11.1 (d) Trigonometric Ratio of Complementary Angles :
| $\sin (90-\theta)=\cos \theta$ | $\cos (90-\theta)=\sin \theta$ |
|---|---|
| $\tan (90-\theta)=\cot \theta$ | $\cot (90-\theta)=\tan \theta$ |
| $\sec (90-\theta)=cosec \theta$ | $cosec(90-\theta)=\sec \theta$ |
$$$$
TRIGONOMETRY
ILLUSTRATIONS :
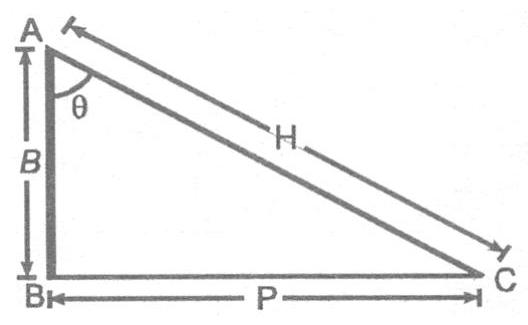
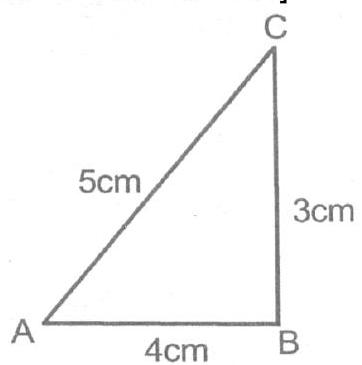
Ex. 1 In the given triangle $AB=3 cm$ and $AC=5 cm$. Find all trigonometric ratios.
TRIGONOMETRY
Sol. Using Pythagoras theorem
$ \begin{aligned} & A C^{2}=A B^{2}+B C^{2} \\ & \Rightarrow \quad 5^{2}=3^{2}+p^{2} \\ & \Rightarrow \quad 16=p^{2} \quad \Rightarrow \quad P=c m \\ & \text { Here } P=4 cm, B=3 cm, H=5 cm \\ & \therefore \quad \sin \theta=\frac{P}{H}=\frac{4}{5} \\ & \cos \theta=\frac{B}{H}=\frac{3}{5} \\ & \tan \theta=\frac{P}{B}=\frac{4}{3} \\ \end{aligned} $
TRIGONOMETRY
$ \begin{aligned} & \cot \theta=\frac{B}{P}=\frac{3}{4} \\ & \sec \theta=\frac{H}{B}=\frac{5}{3} \\ & cosec \theta=\frac{H}{P}=\frac{5}{4} \end{aligned} $
TRIGONOMETRY
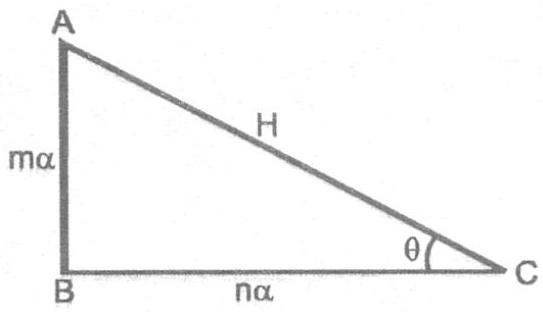
Ex. 2 If $\tan \theta=\frac{m}{n}$, then find $\sin \theta$.
TRIGONOMETRY
Sol. Let $P=m \alpha$ and $B=n \alpha$
$ \begin{matrix} \therefore \quad & \tan \theta=\frac{P}{B}=\frac{m}{n} \\ & H^{2}=P^{2}+B^{2} \\ & H^{2}=m^{2} \alpha^{2}+n^{2} \alpha^{2} \\ & H=\alpha \sqrt{m^{2}+n^{2}} \\ \therefore \quad & \tan \theta=\frac{P}{H}=\frac{m a}{a \sqrt{m^{2}+n^{2}}} \\ & \sin \theta=\frac{m}{\sqrt{m^{2}+n^{2}}} \end{matrix} $
TRIGONOMETRY
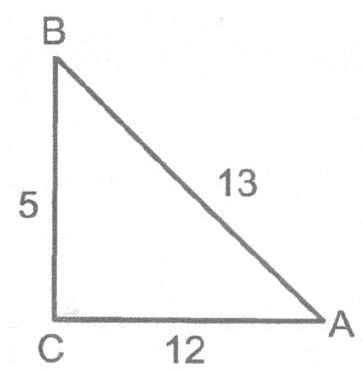
Ex. 3 If $cosec A=\frac{13}{5}$ the prove than $\tan ^{2} A-sing^{2} A=\sin ^{4} A \sec ^{2} A$.
TRIGONOMETRY
Sol. We hare coses $A=\frac{13}{5}=\frac{\text { Hypotenuse }}{\text { Perpendicular }}$
So, we draw a right triangle $A B C$, right angled at $C$ such that hypotenuse $A B=13$ units and perpendicular
$BC=5$ units
$B$ Pythagoras theorem,
$ \begin{aligned} & A B^{2}=B C^{2}+A C^{2} \Rightarrow(13)^{2}=(5)^{2}+A C^{2} \\ & A C^{2}=169-25=144 \\ & A C=\sqrt{144}=12 \text { units } \\ & \qquad \tan A=\frac{B C}{A C}=\frac{5}{12} \\ & \sin A=\frac{B C}{A B}=\frac{5}{13} \\ & \text { and } \sec A=\frac{A B}{A C}=\frac{13}{12} \end{aligned} $
TRIGONOMETRY
L.H.S. $\tan ^{2} A-Sin^{2} A$
$=(\frac{5}{12})^{2}-(\frac{5}{13})^{2}$
$=\frac{25}{144}-\frac{25}{169}$
$=\frac{25(169-144)}{144 \times 169}$
$=\frac{25 \times 25}{144 \times 169}$
TRIGONOMETRY
R.H.S. $=\sin ^{4} A \times \sec ^{2} A$
$=(\frac{5}{13})^{4} \times(\frac{13}{12})^{2}$
$=\frac{5^{4} \times 13^{2}}{13^{4} \times 12^{2}}$
$=\frac{5^{4}}{13^{2} \times 12^{2}}$
$=\frac{25 \times 25}{144 \times 169}$
So, L.H.S. = R.H.S.
Hence Proved.
TRIGONOMETRY
Ex. 4 In $\triangle A B C$, right angled at $B . A C+A B=9 cm$. Determine the value of $\cot C, cosec C, \sec C$.
TRIGONOMETRY
Sol. In $\triangle A B C$, we have $(A C)^{2}=(A B)^{2}+B C^{2}$
$\Rightarrow \quad(9-A B)^{2}=A B^{2}+(3)^{2}$ $[\because A C+A B=9 cm \Rightarrow A C=9-A B]$
$\Rightarrow \quad(81+A B^{2}-18 A B=A B^{2}+9.$
$\Rightarrow \quad 72-18 AB=0$
$\Rightarrow \quad AB=\frac{72}{18}=4 cm$.
TRIGONOMETRY
Now, $\quad A C+A B=9 cm$
$ A C=9-4=5 cm $
So, $\cot C=\frac{B C}{A B}=\frac{3}{4}, cosec C=\frac{A C}{A B}=-\frac{5}{4}, \sec C=\frac{A C}{B C}=\frac{5}{3}$.
TRIGONOMETRY
Ex. 5 Given that $\cos (A-B)=\cos A \cos B+\sin B$, find the value of $\cos 15^{\circ}$.
TRIGONOMETRY
Sol. Putting $A=45^{\circ}$ and $B=30^{\circ}$
We get $\cos (45^{\circ}-30^{\circ})=\cos 45^{\circ} \cos 30^{\circ}+\sin 45^{\circ} \sin 30^{\circ}$
$\Rightarrow \quad \cos 15^{0 .}=\frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2}+\frac{1}{\sqrt{2}} \times \frac{1}{2}$ $\Rightarrow \quad \cos 15^{\circ}=\frac{\sqrt{3}+1}{2 \sqrt{2}}$
TRIGONOMETRY
Ex. 6 A Rhombus of side of $10 cm$ has two angles of $60^{\circ}$ each. Find the length of diagonals and also find its area.
TRIGONOMETRY
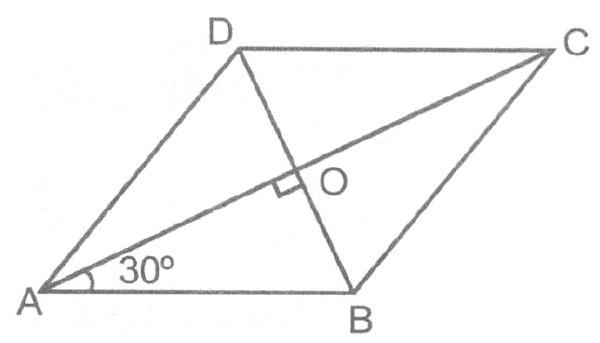
Sol. Let $A B C D$ be a rhombus of side $10 cm$ and $\angle B A D=\angle B C D=60^{\circ}$. Diagonals of parallelogram bisect each other.
$S, A O=O C$ and $B O=O D$
In right triangle $A O B$
$ \sin 30^{\circ}=\frac{OB}{AB} \quad \quad \quad \quad \quad\quad \cos 30^{\circ}=\frac{OA}{AB}$
$\Rightarrow \quad \frac{1}{2}=\frac{OB}{10} $ $\quad \quad \quad \quad \quad\quad \Rightarrow \frac{\sqrt{3}}{2}=\frac{OA}{10} $
$\Rightarrow \quad OB=5 cm \quad \quad \quad \quad \quad\quad \Rightarrow OA=5 \sqrt{3} $
$\therefore \quad BD=2(OB) \quad \quad \quad \quad \quad\quad \Rightarrow AC=2(OA) $
$\Rightarrow \quad BD=2(5) \quad \quad \quad \quad \quad\quad \Rightarrow AC=2(5 \sqrt{3}) $
$\Rightarrow \quad BD=10 cm \quad \quad \quad \quad \quad\quad \Rightarrow AC=10 \sqrt{3} cm $
TRIGONOMETRY
So, the length of diagonals $A C=10 \sqrt{3} cm $&$ B D=10 cm$
Area of Rhombus $=\frac{1}{2} \times AC \times BD$
$ =\frac{1}{2} \times 10 \sqrt{3} \times 10 \quad=50 \sqrt{3} cm^{2} . $
TRIGONOMETRY
Ex. 7 Evaluate : $\frac{\sec ^{2} 54^{0}-\cot ^{2} 36^{\circ}}{cosec^{2} 57^{0}-\tan ^{2} 33^{0}}+2 \sin ^{2} 38^{\circ} \sec ^{2} 52^{\circ}-\sin ^{2} 45^{\circ}+\frac{2}{\sqrt{3}} \tan 17^{0} \tan 60^{\circ} \tan 73^{\circ}$
TRIGONOMETRY
Sol. $ \frac{\sec ^{2} 54^{0}-\cot ^{2} 36^{0}}{cosec^{2} 57^{0}-\tan ^{2} 33^{0}}+2 \sin ^{2} 38^{0} \sec ^{2} 52^{\circ}-\sin ^{2} 45^{\circ}+\frac{2}{\sqrt{3}} \tan 17^{0} \tan 60^{0} \tan 73^{0}$
$=\frac{\sec ^{2}(90^{0}-36^{\circ})-\cot ^{2} 36^{0}}{cosec(90^{0}-33^{0})-\tan ^{2} 33^{0}}+2 \sin ^{2} 38^{0} \sec ^{2}(90^{\circ}-38^{0})-\sin ^{2} 45^{\circ}+\frac{2}{\sqrt{3}} \tan (90^{\circ}-73^{0}) \tan 73^{0} \tan 60^{\circ}$
$=\frac{cosec^{2} 36^{0}-\cot ^{2} 36^{0}}{\sec ^{2} 33^{0}-\tan ^{2} 33^{0}}+2 \sin ^{2} 38^{0} cosec^{2} 38^{0}-(\frac{1}{\sqrt{2}})^{2}+\frac{2}{\sqrt{3}} \cot 73^{0} \tan 73^{0} \times \sqrt{3}$
$=\frac{1}{1}+2 \sin ^{2} 38^{0} \times \frac{1}{\sin ^{2} 38^{0}}-\frac{1}{2}+\frac{2}{\sqrt{3}} \times \frac{1}{\tan 73^{0}} \times 73^{0} \times \sqrt{3}[\because cosec^{2} \theta-\cot ^{2} \theta=1, \sec ^{2} \theta-\tan ^{2} \theta=1]$
$=1+2-\frac{1}{2}+2=5-\frac{1}{2}=\frac{9}{2}$.
TRIGONOMETRY
Ex. 8 Prove that : $cosec(65^{\circ}+\theta)-\sec (25^{\circ}-\theta)-\tan (55^{\circ}-\theta)+\cot (35^{\circ}+\theta)=0$
TRIGONOMETRY
Sol. $\quad cosec(65^{\circ}+\theta)=cosec{90^{0}-(25^{0}-\theta)}=\sec (25^{\circ}-\theta)$ …(i)
$\cot (35^{\circ}+\theta)=\cot {90^{\circ}-(55^{\circ}-\theta)}=\tan (55^{\circ}-\theta)$…(ii)
$\therefore$ L.H.S. $cosec(65^{\circ}+\theta)-\sec (25^{\circ}-\theta)-\tan (55^{\circ}-\theta)+\cot (35^{\circ}+\theta)$
$=\sec (25^{\circ}-\theta)-\sec (25^{\circ}-\theta)-\tan (55^{\circ}-\theta)+\tan (55^{\circ}-\theta)$
$=0[u \ sin \ g(i) $&$(ii)]$ R.H.S.
TRIGONOMETRY
Ex. 9 Prove that : $\cot \theta-\tan \theta=\frac{2 \cos ^{2} \theta-1}{\sin \theta \cos \theta}$
TRIGONOMETRY
Sol. L.H.S. $\cot \theta-\tan \theta$
$=\frac{\cos \theta}{\sin \theta}-\frac{\sin \theta}{\cos \theta}$ $\quad \quad \quad [\because \cot \theta=\frac{\cos \theta}{\sin \theta}, \tan \theta=\frac{\sin \theta}{\cos \theta}]$
$=\frac{\cos ^{2} \theta-\sin ^{2}}{\sin \theta \cos \theta} \quad=\frac{\cos ^{2} \theta-(1-\cos ^{2} \theta)}{\sin \theta \cos \theta}$ $\quad \quad \quad [\because \sin ^{2} \theta=1-\cos ^{2} \theta]$
$=\frac{\cos ^{2} \theta-1+\cos ^{2} \theta}{\sin \theta \cos \theta}=\frac{2 \cos ^{2} \theta-1}{\sin \theta \cos \theta}$ R.H.S. Hence Proved.
TRIGONOMETRY
Ex. 10 Prove that: $(coses A-\sin A)(\sec A-\cos A)(\tan A+\cot A)=1$.
TRIGONOMETRY
Sol. L.H.S. $(cosec A-\sin A)(\sec A-\cos A)(\tan A+\cot A)$
$ =(\frac{1}{\sin A}-\sin A)(\frac{1}{\cos A}-\cos A)(\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}) $
$ =(\frac{1-\sin ^{2} A}{\sin A})(\frac{1-\cos ^{2} A}{\cos A})(\frac{\sin ^{2} A+\cos ^{2} A}{\sin A \cos A}) $
$ =(\frac{\cos ^{2} A}{\sin A})(\frac{\sin ^{2} A}{\cos A})(\frac{1}{\sin A \cos A})$ $[\because \sin ^{2} A+\cos ^{2} A=1]$
$ =1 $
R.H.S. Hence Proved
TRIGONOMETRY
Ex. 11 If $\sin \theta+\cos \theta=m$ and $\sec \theta+cosec \theta=n$, then prove that $n(m^{2}-1)=2 m$.
TRIGONOMETRY
Sol. L.H.S. $n(m^{2}-1)$
$ \begin{matrix} =(\sec \theta + cosec \theta)[(\sin \theta+\cos \theta)^{2}-1] =(\frac{1}{\cos \theta}+\frac{1}{\sin \theta})(\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta-1) \\ =(\frac{\cos \theta+\sin \theta}{\sin \theta \cos \theta})(1+2 \sin \theta \cos \theta-1) =\frac{(\cos \theta+\sin \theta)}{\sin \theta \cos \theta}(2 \sin \theta \cos \theta) \end{matrix} $
$ =2(\sin \theta+\cos \theta) \quad=2 m \quad \text {R.H.S.} \quad \text { Hence Proved. } $
TRIGONOMETRY
Ex. 12 If $\sec \theta=x+\frac{1}{4 x}$, then prove that $\sec \theta+\tan \theta=2 x$ or $\frac{1}{2 x}$.
TRIGONOMETRY
Sol. $\quad \sec \theta=x+\frac{1}{4 x}$ …(i)
$ \begin{aligned} & \therefore \quad 1+\tan ^{2} \theta=\sec ^{2} \theta \\ & \Rightarrow \quad \tan ^{2} \theta=\sec ^{2} \theta-1 \quad \Rightarrow \quad \tan ^{2} \theta=(x+\frac{1}{4 x})^{2}-1 \\ & \Rightarrow \quad \tan ^{2} \theta=x^{2}+\frac{1}{16 x^{2}}+2 \times x \times \frac{1}{4 x}-1 \\ & \Rightarrow \quad \tan ^{2} \theta=x^{2}+\frac{1}{16 x^{2}}+\frac{1}{2}-1 \quad \Rightarrow \quad \tan \theta= \pm(x-\frac{1}{4 x}) \\ & \Rightarrow \quad \tan ^{2} \theta=(x-\frac{1}{4 x})^{2} \quad \Rightarrow \quad \tan \theta= \pm(x-\frac{1}{4 x}) \\ & \text { So, } \quad \tan \theta=x-\frac{1}{4 x} …(ii)\\ & \text { or } \tan \theta=-(x-\frac{1}{4 x}) …(iii) \end{aligned} $
TRIGONOMETRY
Adding equation (i) and (ii)
$ \sec \theta+\tan \theta=x+\frac{1}{4 x}+x-\frac{1}{4 x} $
$ \sec \theta+\tan \theta=2 x $
Adding equation (i) and (ii)
$ \begin{aligned} & \sec \theta+\tan \theta=x+\frac{1}{4 x}-x+\frac{1}{4 x} \\ & \quad=\frac{1}{2 x} \quad \text { Hence, } \sec \theta+\tan \theta+2 x \text { or } \frac{1}{2 x} . \end{aligned} $
Ex. 13 If $\theta$ is an acute angle and $\tan \theta+\cot \theta=2$ find the value of $\tan ^{9} \theta+\cot ^{9} \theta$
TRIGONOMETRY
Sol. We have, $\tan \theta+\cot \theta=2$
$\Rightarrow \quad \tan \theta+\frac{1}{\tan \theta}=2 $
$\Rightarrow \quad \tan ^{2} \theta+1=2 \tan \theta $
$\Rightarrow \quad(\tan \theta-1)^{2}=0 $
$\Rightarrow \quad \tan \theta=1 $
$\therefore \tan ^{9} \theta+\cot ^{9} \theta $
$=\tan ^{9} 45^{0}+\cot ^{9} 45^{0} $
$=\quad(1)^{9}+(1)^{9} $
TRIGONOMETRY
$\Rightarrow \quad \frac{\tan ^{2} \theta+1}{\tan \theta}=2 $
$\Rightarrow \quad \tan ^{2} \theta-2 \tan \theta+1=0 $
$\Rightarrow \quad \tan \theta-1=0 $
$\quad \Rightarrow \tan \theta=\tan 45^{0}$ $\quad \Rightarrow \theta = 45^{0}$
$=\quad(\tan 45)^{9}+(\cot 45)^{0}$
$\quad =2 \text {. }$
TRIGONOMETRY
DAILY PRACTIVE PROBLEMS 11
OBJECTIVE DPP - 11.1
1. If $\alpha+\beta=\frac{\pi}{2}$ and $\alpha=\frac{1}{3}$, then $\sin \beta$ is
(A) $\frac{\sqrt{2}}{3}$ $\quad$
(B) $\frac{2 \sqrt{2}}{3}$ $\quad$
(C) $\frac{2}{3}$ $\quad$
(D) $\frac{3}{4}$
TRIGONOMETRY
| Qus. | 1 |
|---|---|
| Ans. | B |
TRIGONOMETRY
2. If $5 \tan \theta=4$, then value of $\frac{5 \sin \theta-3 \cos \theta}{5 \sin \theta+2 \cos \theta}$ is
(A) $\frac{1}{3}$ $\quad$
(B) $\frac{1}{6}$ $\quad$
(C) $\frac{4}{5}$ $\quad$
(D) $\frac{2}{3}$
TRIGONOMETRY
| Qus. | 2 |
|---|---|
| Ans. | B |
TRIGONOMETRY
3. If $7 \sin \alpha=24 \cos \alpha ; 0<\alpha<\frac{\pi}{2}$, then value of $14 \tan \alpha-75 \cos \alpha-7 \sec \alpha$ is equal to
(A) 1 $\quad$
(B) 2 $\quad$
(C) 3 $\quad$
(D) 4
TRIGONOMETRY
| Qus. | 3 |
|---|---|
| Ans. | B |
TRIGONOMETRY
4. Given $3 \beta+5 \cos \alpha ; \beta=5$, then the value of $(3 \cos \beta-5 \sin \beta)^{2}$ is equal to
(A) 9 $\quad$
(B) $\frac{9}{5}$ $\quad$
(C) $\frac{1}{3}$ $\quad$
(D) $\frac{1}{9}$
TRIGONOMETRY
| Qus. | 4 |
|---|---|
| Ans. | A |
TRIGONOMETRY
5. If $\tan \theta=4$, then $(\frac{\tan \theta}{\frac{\sin ^{3} \theta}{\cos \theta}+\sin \theta \cos \theta})$ is equal to
(A) 0 $\quad$
(B) $2 \sqrt{2}$ $\quad$
(C) $\sqrt{2}$ $\quad$
(D) 1
TRIGONOMETRY
| Qus. | 5 |
|---|---|
| Ans. | D |
TRIGONOMETRY
6. The value of $\tan 5^{\circ} \tan 10^{\circ} \tan 15^{\circ} 20^{\circ}$ $\tan 85^{\circ}$, is
(A) 1 $\quad$
(B) 2 $\quad$
(C) 3 $\quad$
(D) None of these
TRIGONOMETRY
| Qus. | 6 |
|---|---|
| Ans. | A |
TRIGONOMETRY
7. As $x$ increases from 0 to $\frac{\pi}{2}$ the value of $\cos x$
(A) increases $\quad$
(B) decreases $\quad$
(C) remains constant $\quad$
(D) increases, then decreases
TRIGONOMETRY
| Qus. | 7 |
|---|---|
| Ans. | B |
TRIGONOMETRY
8. Find the value of $x$ from the equation $x \sin \frac{\pi}{6} \cos ^{2} \frac{\pi}{4}=\frac{\cot ^{2} \frac{\pi}{6} \sec \frac{\pi}{3} \tan \frac{\pi}{4}}{cosec^{2} \frac{\pi}{4} cosec \frac{\pi}{6}}$
(A) 4 $\quad$
(B) 6 $\quad$
(C) - 2 $\quad$
(D) 0
TRIGONOMETRY
| Qus. | 8 |
|---|---|
| Ans. | B |
TRIGONOMETRY
9. The area of a triangle is $12 sq . cm$. Two sides are $6 cm$ and $12 cm$. The included angle is
(A) $\cos ^{-1}(\frac{1}{3})$ $\quad$
(B) $\cos ^{-1}(\frac{1}{6})$ $\quad$
(C) $\sin ^{-1}(\frac{1}{6})$ $\quad$
(D) $\sin ^{-1}(\frac{1}{3})$
TRIGONOMETRY
| Qus. | 9 |
|---|---|
| Ans. | D |
TRIGONOMETRY
10. If $\alpha+\beta=90^{\circ}$ and $\alpha=2 \beta$ then $\cos ^{2} \alpha+\sin ^{2} \beta$ equals to
(A) $\frac{1}{2}$ $\quad$
(B) 0 $\quad$
(C) 1 $\quad$
(D) 2
TRIGONOMETRY
| Qus. | 10 |
|---|---|
| Ans. | A |
TRIGONOMETRY
SUBJECTIVE DPP - 11.2
1. Evaluate : (A) $\frac{\sin \theta \cos \theta \sin (90^{\circ}-\theta)}{\cos (90^{\circ}-\theta)}+\frac{\cos \theta \sin \theta \cos (90^{\circ}-\theta)}{\sin (90^{\circ}-\theta)}+\frac{\sin ^{2} 27^{\circ}+\sin ^{2} 63^{\circ}}{\cos ^{2} 40^{\circ}+\cos ^{2} 50^{\circ}}$
(B) $\cos 10^{\circ} \cos 2^{\circ} \cos 3^{\circ} ——– \cos 180^{\circ}$
(C) $\sin (50^{\circ}+\theta)-\cos (40^{\circ}-\theta)+\tan 1^{0} \tan 20^{\circ} \tan 70^{\circ} \tan 80^{\circ} \tan 89^{\circ}$
(D) $\frac{2}{3}(\cos ^{4} 30^{\circ}-\sin ^{4} 45^{\circ})-3(\sin ^{2} 60^{\circ}-\sec ^{2} 45^{\circ})+\frac{1}{4} \cot ^{2} 30^{0}$
(E) $\frac{\cos ^{2} 20^{\circ}+\cos ^{2} 70^{\circ}}{\sec ^{2} 50-\cot ^{2} 40^{\circ}}+2 cosec{ }^{2} 58^{\circ}-2 \cot 58^{\circ} \tan 32^{\circ}-4 \tan 13^{0} \tan 37^{\circ} \tan 45^{\circ} \tan 53^{\circ} \tan 77^{\circ}$
TRIGONOMETRY
| Qus. 1 | Ans. |
|---|---|
| (A) | 2 |
| (B) | 0 |
| (C) | 1 |
| (D) | $\frac{113}{24}$ |
TRIGONOMETRY
2. If $\cot \theta=\frac{3}{4}$, prove that $\sqrt{\frac{\sec \theta-cosec \theta}{\sec \theta+cosec \theta}}=\frac{1}{\sqrt{7}}$.
TRIGONOMETRY
3. If $A+B=90^{\circ}$, prove that : $\sqrt{\frac{\tan A \tan B+\tan A \cot B}{\sin A \sec B}-\frac{\sin ^{2} B}{\cos ^{2} A}}=\tan A$
TRIGONOMETRY
4. If $A, B, C$ are the interior angles of a $\triangle A B C$, show that :
(i) $\sin \frac{B+C}{2}=\cos \frac{A}{2}$ $\quad$ (ii) $\cos \frac{B+C}{2}=\sin \frac{A}{2}$
TRIGONOMETRY
Prove the following (Q, 5 to Q. 13)
5. $\tan ^{2} \theta-\sin ^{2} \theta=\tan ^{2} \theta \sin ^{2} \theta$
TRIGONOMETRY
6. $\quad(\sin \theta+cosec \theta)+(\cos \theta+\sec \theta)^{2}=7+\tan ^{2} \theta+\cot ^{2} \theta$
[CBSE - 2008]
TRIGONOMETRY
7. $\frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}=\sec \theta cosec \theta+1$
TRIGONOMETRY
8. $\sqrt{\frac{1-\sin \theta}{1+\sin \theta}}=\sec \theta-\tan \theta$
TRIGONOMETRY
9. $\frac{\sin A+\cos A}{\sin A+\cos A}+\frac{\sin A-\cos A}{\sin A+\cos A}=\frac{2}{\sin ^{2} A-\cos ^{2} A}=\frac{2}{1-2 \cos ^{2} A}$
TRIGONOMETRY
10. $\quad(\sin \theta+\sec \theta)^{2}+(\cos \theta+cosec \theta)^{2}=(1+\sec \theta$ $cosec \theta)^{2}$
TRIGONOMETRY
11. $(1+\cot \theta-cosec \theta)(1+\tan \theta+\sec \theta)=2$
TRIGONOMETRY
12. $\quad(\sin ^{8} \theta-\cos ^{8} \theta)=(\sin ^{2} \theta-\cos ^{2} \theta)(1-2 \sin ^{2} \theta \cos ^{2} \theta)$
TRIGONOMETRY
13. $\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}$
TRIGONOMETRY
14. If $x=r \sin \theta \cos \phi, y=r \sin \theta \sin \phi, z=r \cos \theta$, then Prove that : $x^{2}+y^{2}+z^{2}=r^{2}$.
TRIGONOMETRY
15. If $\cot \theta+\tan \theta=x$ and $\sec \theta-\cos \theta=y$, then prove that $(x^{2} y)^{2 / 3}-(x y^{2})^{2 / 3}=1$
TRIGONOMETRY
16. If $\sec \theta+\tan \theta=p$, then show that $\frac{p^{2}-1}{p^{2}+1}=\sin \theta$
[CBSE - 2004]
TRIGONOMETRY
17. Prove that : $\tan ^{2} A-\tan ^{2} B=\frac{\cos ^{2} B-\cos ^{2} A}{\cos ^{2} B \cos ^{2} A}=\frac{\sin ^{2} A-\sin ^{2} B}{\sin ^{2} A \sin ^{2} B}$
[CBSE - 2005]
TRIGONOMETRY
18. Prove that : $\frac{1}{\sec x-\tan x}-\frac{1}{\cos x}=\frac{1}{\cos x}=\frac{1}{\cos x}-\frac{1}{\sec x+\tan x}$
[CBSE - 2005]
TRIGONOMETRY
19. Prove : $(1+\tan ^{2} A)+(1+\frac{1}{\tan ^{2} A})=\frac{1}{\sin ^{2} A-\sin ^{4} A}$
[CBSE - 2006]
TRIGONOMETRY
20. Evaluate :
$\tan 7^{\circ} \tan 23^{\circ} \tan 60^{\circ} \tan 67^{\circ} \tan 83^{\circ}+\frac{\cot 54^{\circ}}{\tan 36^{\circ}}+\sin 20^{\circ} \sec 70^{\circ}-2$.
[CBSE - 2007]
TRIGONOMETRY
| Qus. | 20 |
|---|---|
| Ans. | $\sqrt {3}$ |
TRIGONOMETRY
21. Without using trigonometric tables, evaluate the following :
$(\sin ^{2} 65^{\circ}+\sin ^{2} 25^{\circ})+\sqrt{3}(\tan 5^{\circ} \tan 15^{\circ} \tan 30^{\circ} \tan 75^{\circ} \tan 85^{\circ})$
[CBSE - 2008]
TRIGONOMETRY
| Qus. | 21 |
|---|---|
| Ans. | 2 |
TRIGONOMETRY
22. If $\sin 3 \theta=\cos (\theta-60^{\circ})$ and $3 \theta$ and $\theta-60^{\circ}$ are acute, find the value of $\theta$
[CBSE - 2008]
TRIGONOMETRY
| Qus. | 22 |
|---|---|
| Ans. | $24^\circ$ |
TRIGONOMETRY
23. If $\sin \theta=\cos \theta$, find the value of $\theta$.
[CBSE - 2008]
TRIGONOMETRY
| Qus. | 23 |
|---|---|
| Ans. | $45^\circ$ |
TRIGONOMETRY
24. If $7 \sin ^{2} \theta+3 \cos ^{2} \theta=4$, show that $\tan \theta=\frac{1}{\sqrt{3}}$
[CBSE - 2008]
TRIGONOMETRY
25. Prove : $\sin \theta(1+\tan \theta)+\cos \theta(1+\cot \theta)=\sec \theta+cosec \theta$.





